Pete Stewart offers an introduction to the mysteries of transposing music written in different keys for pipers who find themselves newly facing the world of music beyond the pipe band.

(Please note; this article contained a number of inaccuracies and typesetting errors; they were corrected in the december 2016 issue)

Some years ago, in response to a number of occasions on which I heard pipers stumble to answer questions like ‘What key are you playing in?’, I compiled, in association with one or two pipers who had found themselves in such a situation, a brief tutor on the basics of keys and their relationships. It has lain unattended on the LBPS website ever since..
The original ‘tutor’ made no assumptions about previous knowledge of this matter, and therefore probably contains material familiar to many. If you are a complete newcomer to non-piping music theory, then you may want to hunt down the first parts of this tutor; (http://tinyurl.com/hzlnmff). I have left in place here several references to matters covered in the earlier sections.
The original tutor was based around three tunes from Machlachlan’s The Piper’s Assistant; chosen because each  is written in a different key. Here I have extracted the later section of the tutor which introduces the notion of ‘transposing’, converting music written in one key so that it can be played in another. This is a challenge that pipers may increasingly face as their repertoire is expanded by playing alongside other instruments.

So you have the makings of an understanding of what key you are playing your GHB, smallpipe or border pipe chanter in. But what happens if you decide to play on your A chanter music written out for instruments in other keys – D, G, C, F Bflat; fiddle music, for instance, might be in any of these or other keys. This music will at first look alien; we are going to explore how to come to terms with it. First, consider the three key signatures we have worked with:

It is clear there is a pattern here; each scale is related to the one before and after by the interval of a fifth. If we extend this sequence  in both directions we will eventually find ourselves in a circle (‘the circle of fifths’) However, for our purposes we need only deal with four or five of the twelve; going down from D & G by fifths introduces C and F scales; we will work with these four since they are the ones you are most likely to meet.  
Going down a fifth form G brings us to C; to retain the ‘major’ scale intervals (tone-tone-semitone-tone-tone-tone-semitone-tone] we must lower the fourth note, F, by a semi-tone, ie. Remove the sharp from the key-signature, which is now ‘empty
Similarly, moving down another fifth, we reach F. Lowering the fourth (B) here requires the introduction of a ‘flat’ symbol - b, and this sign will appear in the key signature.
F    G    A    Bb    C    D    E    F

Equipped with this understanding, we can now return to the tune Robertson’s Quickstep (Fig. 4) as written out, in the key of D, in McLachlan’s collection.

Fig 4

The notes of this tune are such that we can play it on a GHB chanter; however, here is another version of the tune which we cannot play on the GHB chanter.

Fig 5

A fiddle player will have no difficulty playing from this music; they will, however, be playing a fifth lower than before, in the key of G. For a piper to play along, they will need a different chanter, one whose ‘six-finger’ note is D, rather than A. A GHB piper could play this D chanter reading from the GHB music, ‘pretending’ they were playing in the usual way; the only difference would be that what they were now playing would sound a fifth lower.
 However, the task our piper has set themself is to learn to play the A chanter [or, indeed, any other pitch of chanter] from music written for some other instrument [an English bagpipe collection, say, published for chanters in D]. Fig 5 is an example, and this is another, The 42nd Highlanders Farewell to Gibraltar [from Maclachlan’s Piper’s Assistant], in the key of D rather than A.

Fig 6

How does our piper learn to read and play this? Basically they must understand pretty well the material we covered in the previous sections, how the chanter scale relates to the key signature. Then they must tackle the manner in which the tune is built out of the scale and how this relates to the fingering of the chanter. Once the structure of the tune in one scale can be grasped, then it will become possible to transfer this structure from one scale to another.
It’s worth reassuring ourselves that this task is made immensely easier because we have only nine notes to deal with in any one scale or structure; imagine having to learn how to apply this to all 12 keys and all seven octaves, as a pianist would have to do.
Before proceeding, perhaps we should identify the notes that appear in this music that GHB pipers may not have met before. I have labelled them as they appear in the second four bars of the tune;      
 

Fig 7

Structure
The next task is to analyse how the tune is built. It is done by putting together blocks of notes, blocks which themselves consist of small patterns. Pipers who have experience of playing a number of tunes will be aware that they often find themselves playing the same little patterns repeatedly in different tunes; if you have not had this experience, then you are going to get it now, because we will begin by looking at these ‘blocks’ as they occur in the tunes we have considered so far.
The most fundamental of these ‘blocks’, and among the shortest, is the ‘octave’.  If we understand the information contained in the key signature we can identify what this octave should be even if it does not actually appear as a ‘block’ in the tune.
Look at notes iv,v & vi in bar 1 of Fig. 7: [ bar 1 is the first full bar.]

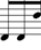
In this case the octave is indeed the basic one of the ‘key’, D major; the block is the beginning and end of the scale of D. We can consider this as the ‘outer frame’ of our tune’s structure [although we will often step outside this outer frame].
One of the benefits of using the pipe chanter to learn this stuff is that there are only two possible octaves available; on the GHB chanter these are A-a and G-g. In our tune here they are D-d and C-c [You may find yourself wanting to play music written for an instrument that can also play an octave C#-c# - I shall not deal with that possibility now – it will cause complications which you should beware of; basically a smallpipe or a GHB chanter cannot reproduce such music without modification, though most border pipe chanters can.]
So, we have two octave blocks, one of which, by referring to our key signature, we have identified as forming the ‘boundaries’ of our scale. It so happens that in this tune we also have an example of the other octave, notes v & vi of bar three
C-c, the equivalent in the key of D to the smallpipe G-g octave.

So, by understanding the key signature and relating this to the notes of the tune, we have identified, first our ‘six-finger’ note, and then our ‘seven-finger’ note, as well as their relative octaves; that’s four notes out of nine, nearly half-way and all we’ve done is look at the key signature and two notes …
Now, in our discussion of the relationship between keys we identified the interval of a fifth as being crucial, it bearing the next closest relationship to the root after the octave.
We can see this interval in our D tune bar 2, notes iii & iv. A-D.

It is as if the A stands in the middle of the scale, between the D and the d. Between the A and the D in this sequence we find an F#. The interval between the D and the A we know is called the ‘fifth’; that between the D and the F# is the ‘third’, since the F# is the third note in the D major scale.
So these simple mathematical ratios have built us a further subdivision of our octave; we now have D-F#-A-d

Let’s look again at this tune in A:
We can see here that the ‘block’ we have identified [bar 2, notes i- iv] is constructed from the notes A-C#-E-a, our six-finger, four-finger, two-finger and open notes. We can therefore translate this fingering into D-F#-A-d in our D major music. Together with our two octaves this gives us the knowledge to identify 6 of our nine notes.
Finally let’s go back to the C-c octave and look at the first four notes of bar 4 of the ‘D’ version:

The notes here are C–E-G, they have the same relationship between them as the D-F#-A group has [being the 1st, 3rd and 5th of the C octave], they translate into G-B-D on the GHB chanter and they make our total of recognisable notes up to 8. You will have noticed that bars 3 and 4 here are ‘identical’ to bars 1 and 2 - ‘identical’ that is, in their structure, though they are a tone apart.
Now let’s look at the last three notes in bar 1 and the first four in bar 2 [and their equivalent in bars 3 and 4]
We can recognise here our octave and 5th and 3rd; but what about that note iii? It’s a B, the equivalent in the key of D of the ‘F’ in key of A on the GHB..

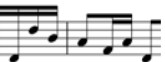
  I am going to say little more about this note here except to observe that the sound of the notes D F# A B  d B A F# will be familiar enough to anyone who has ever listened to a 1950’s rock and roll band. The B is a ‘6th’ and is the equivalent in the key of D to the F# in the key of A.
So now we have identified all our 9 notes using the key signature and the simple intervals of 5th and 3rd.
 
The art of transposing
The whole art of transposing music for bagpipes can be described in two simple processes; first, to familiarise oneself with the relationship between these ‘structural’ intervals and the fingering that produces them and second, to identify these structural intervals in different keys.
Fig. 8 charts these structural units in each of the keys pipers are likely to meet in most instances: the familiar ‘key of A’ is at the top and the chart works down in fifths, and next to each shows the ‘seven-finger octave’ equivalent to that on a GHB or smallpipe chanter: 

Fig. 8

Here are the last two notes of the first bar and the first four notes of the second bar of our tune in each of the keys we are considering, together with their associated 7-finger sequence from bars 3 & 4 [I have included the natural symbols as they would appear with the key signature appropriate for each key]: this pair of sequences contains all the notes on the GHB chanter.

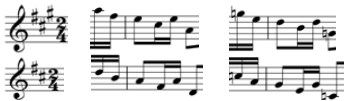
 Try taking other short sections and playing them from each version. Same sound, different notes…
 And here are all four versions

For completeness’ sake, here are the other two tunes we have been considering, in all four keys: These are real challenges, since the ‘original’ keys involve scales that begin in different places – needs some thinking about; to help, I have ordered them so that the familiar GHB version is first

Robertson’s Quickstep
For this tune, the original is in the ‘3-finger’ key. If French or other European pipe music is what you want to play, then you will have to master this challenge, since much of the music is written in this way. As we have seen, this kind of tune can be played on an A chanter although it is written in D. But the challenge is to play it on the GHB or smallpipe chanter when it is written in G or C or even F. As usual, the trick is to identify the octave interval the tune includes, and treat that as the ‘6-finger’ note; the difference is that whilst this octave forms the ‘frame’ of the tune, it is not the octave we should expect from looking at the key signature. Thus, the first example, our original, marked ‘D’, contains an A-a octave, and is thus written for an A chanter; the second example ‘G’ contains the octave D-d, and is written for a ‘D’ chanter - and so on. Notice that for a ‘C’ chanter this tune is written and played in F.

Stormont Lads
The third tune is even more of a challenge, since it is written in the 7-finger key; the trick here is slightly more complex, since we must identify both octaves, treating the upper one as our 6-finger note, since the top note of the upper of the two octaves will be our highest available note. GHB tunes of this sort are rare; moreover, they can only be considered to be in the key I have allocated them because they do not use (or use only in a passing way) the four-finger note, which lies outside the major scale in each key.
However, as this example reveals, it does allow the ‘extra’ 9th note (high B on the A chanter) to be played without any pinching or other device; what is more, the border pipe chanter should allow the four finger note to be lowered by a semi-tone, allowing into the repertoire a wide range of music from both Scottish and other traditions. However, though much of this music may come already written in G (and hence requiring no transposition), it may also come, from the fiddle sources, for instance, in A or D. In this case the challenge in transposing is rather different, though the principles remain the same - identify the highest octave and treat the upper note as if it were a high A.

This has been a rapid canter through the challenges of transposing music from one key to another. Practice, as ever, will serve to make the technique more familiar. As a guide, it is suggested that, once you have read this article and gained an insight into the principles as they apply to all keys, you concentrate on reading music in just one of the keys, probably D or G, since these are the keys you are most likely to meet when playing with other instruments. Once this has become familiar and you have a grasp of the principles involved you will find that it becomes easier to treat music written in other keys in the same way.